Vector Spaces in Machine Learning

As a student learning about linear algebra and its applications in machine learning, vector spaces was just a term I came across in textbooks. It felt distant, somewhat intimidating, like a high-level concept reserved for the mathematically adept. But as I delved deeper, I realized its innate simplicity and its profound relevance to the world of machine learning. 

You know, back in college, I used to think of vectors as arrows pointing in space. And technically, that’s not wrong! But vector spaces? That’s where the beauty of mathematics meets real-world applications.

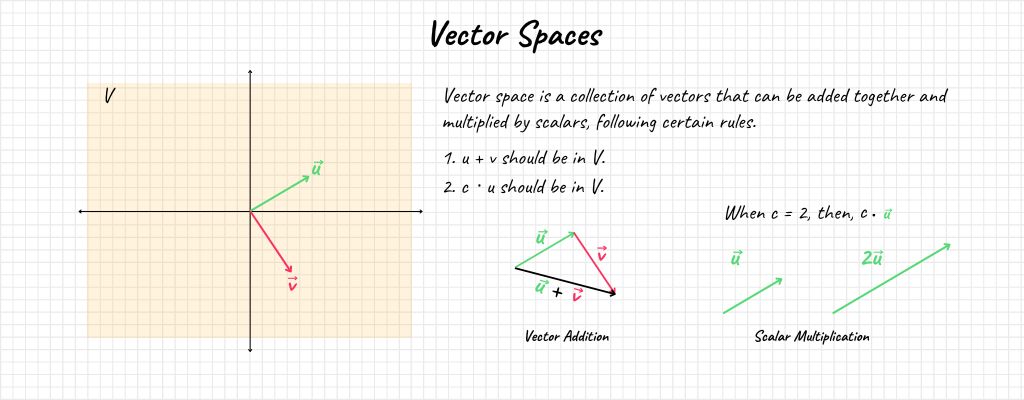
In simple words, a vector space is a collection of vectors. But not just any random collection; they have to abide by specific rules. If you take two vectors from this collection, their addition should still belong to the same space (vector addition). Similarly, if you multiply a vector by a scalar (just a fancy word for a regular number), it should still remain in that space, also known as scalar multiplication.

Mathematically, if we have vectors \( \mathbf{u} \) and \( \mathbf{v} \) in a vector space \( V \), and a scalar \( c \):

1. \( \mathbf{u} + \mathbf{v} \) should be in \( V \).

2. \( c \cdot \mathbf{u} \) should be in \( V \).

As I began diving deeper into machine learning, the data’s abstract nature became evident. How do you represent a sentence, an image, or even a user’s behavior? That’s where vector spaces come in.

In machine learning, we often transform complex data into vectors so that we can perform mathematical operations on them. The ability to represent data in a structured vector space allows us to measure similarities, make predictions, and derive insights. Trust me; once you grasp vector spaces, a lot of machine learning techniques will start making more sense!

By the end of this lesson, I hope to impart to you not just a textbook definition of vector spaces, but an understanding based on real experience. I want you to see why it’s such a fundamental concept in machine learning and how it can be a game-changer in understanding and implementing algorithms.

The Basics of Vector Spaces

Studying linear algebra, I often ask myself why much of the course content focuses on vectors? But the deeper I went, the clearer the picture became. Vectors are fundamental, not just in machine learning but in the vast realm of mathematics and physics. Let’s unravel this together.

Understanding Vectors

You’ve probably come across arrows in diagrams, haven’t you? Think of an arrow pointing in a certain direction with a defined length. This is essentially a vector. In the world of mathematics, a vector is an object that has both a magnitude (how long it is) and a direction (where it’s pointing). *insert vector image here*

For instance, in a 2-dimensional space (like a piece of paper), a vector \( \mathbf{v} \) can be represented as:

\[ \mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \]

where \( v_1 \) and \( v_2 \) are the components along the x and y axes, respectively.

Scalar Multiplication

Imagine you have a rubber arrow (your vector) and you stretch or shrink it. The direction remains unchanged, but its length (magnitude) alters. This stretching or shrinking is the essence of scalar multiplication.

Given a vector \( \mathbf{u} \) and a scalar \( c \), the scalar multiplication is:

\[ c \cdot \mathbf{u} = \begin{bmatrix} c \cdot u_1 \\ c \cdot u_2 \end{bmatrix} \]

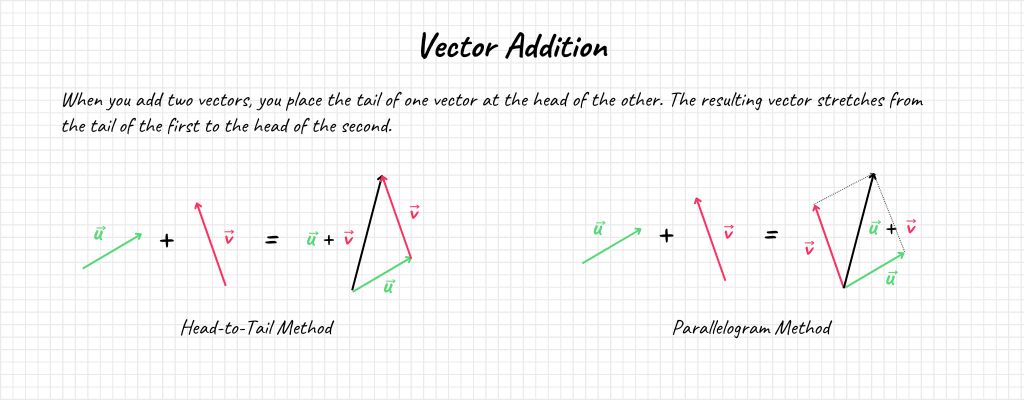
Vector Addition

Vector addition is like playing a lego set – you stack one lego piece on top of the other to arrive at a different structure from your original set. When you add two vectors, you place the tail of one vector at the head of the other. The resulting vector stretches from the tail of the first to the head of the second. 

For two vectors \( \mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} \) and \( \mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \), their addition is:

\[ \mathbf{u} + \mathbf{v} = \begin{bmatrix} u_1 + v_1 \\ u_2 + v_2 \end{bmatrix} \]

The Geometry of Vector Spaces

In the vastness of spaces (and I’m not talking about the cosmos!), vectors reside in structured homes called vector spaces. Imagine an infinite sea of arrows, all originating from one point but stretching out in every possible direction. This is the essence of the geometry of vector spaces.

But there’s a catch: Not all collections of vectors form a vector space. They must adhere to certain rules, ensuring operations like addition and scalar multiplication keep the resultant vectors within the same space.

Insert vector space image here.

Visualization and Interpretation

A picture is worth a thousand words”, they say, and in the world of vectors, this couldn’t be truer. Visualizing vectors and their operations can be a revelation.

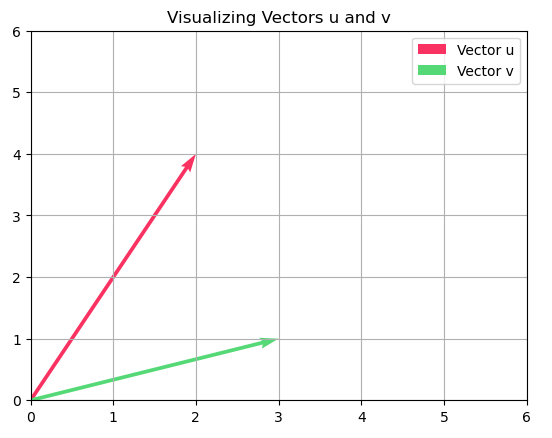
Using Python, with the library matplotlib, let’s visualize a couple of vectors:

import matplotlib.pyplot as plt
import numpy as np

u = np.array([2, 4])
v = np.array([3, 1])

plt.quiver(0, 0, u[0], u[1], angles='xy', scale_units='xy', scale=1, color='r', label='Vector u')
plt.quiver(0, 0, v[0], v[1], angles='xy', scale_units='xy', scale=1, color='b', label='Vector v')
plt.xlim(0, 6)
plt.ylim(0, 6)
plt.grid()
plt.legend()
plt.title("Visualizing Vectors u and v")
plt.show()

When you run this code, you’ll see two arrows – representing our vectors \( \mathbf{u} \) and \( \mathbf{v} \) – originating from the origin and pointing in their respective directions. It’s a simple yet powerful way to interpret and visualize the abstract nature of vectors.

This foundation of vectors is crucial. They’re the building blocks upon which the palace of machine learning stands. As we proceed, remember these basics; they’ll illuminate many complex concepts down the line.

Applications of Vector Spaces in Machine Learning

During my days of tinkering with machine learning models, a realization hit me: Behind every algorithm, be it simple or intricate, lies the concept of vector spaces. I began to see machine learning not just as an ensemble of algorithms, but as a dance of vectors. Let’s delve into this further.

Representing Data as Vectors

It was during a personal project, when I tried to teach a machine to comprehend news articles, that the significance of representing data as vectors dawned on me. Consider this: How would you feed an entire article or a picture into an algorithm?

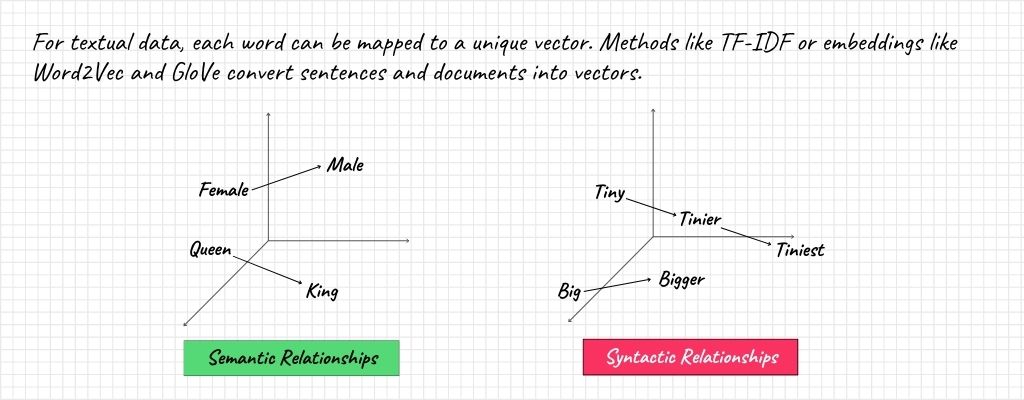
• Text: For textual data, each word can be mapped to a unique vector. Methods like TF-IDF or embeddings like Word2Vec and GloVe convert sentences and documents into vectors. For instance, the sentence “I love machine learning” gets transformed into a set of numbers that machines can understand and process.
• Images: For images, each pixel’s intensity in an image translates to a number. An RGB image can be thought of as three matrices (or 3D array) representing red, green, and blue color intensities. This 3D array is, in essence, our vector representation.
• Sounds, user behavior, sensor data, and more – they all can be distilled into vectors, enabling algorithms to make sense of the world.

Vector Spaces in Algorithms

With data converted to vectors, algorithms can now play. Think of it as providing the rules and moves for the dance of vectors.

• Linear Regression: One of the basic algorithms, yet its core is the dot product of vectors. Given input vectors and weights, predictions are made based on their linear combinations.
• Neural Networks: These are essentially layers and layers of vector transformations. From input to hidden layers, and to the output, at every stage, vectors are transformed, tweaked, and adjusted to model intricate patterns.
• Support Vector Machines: The very name gives it away! SVM tries to find the optimal hyperplane that separates different classes in a vector space.

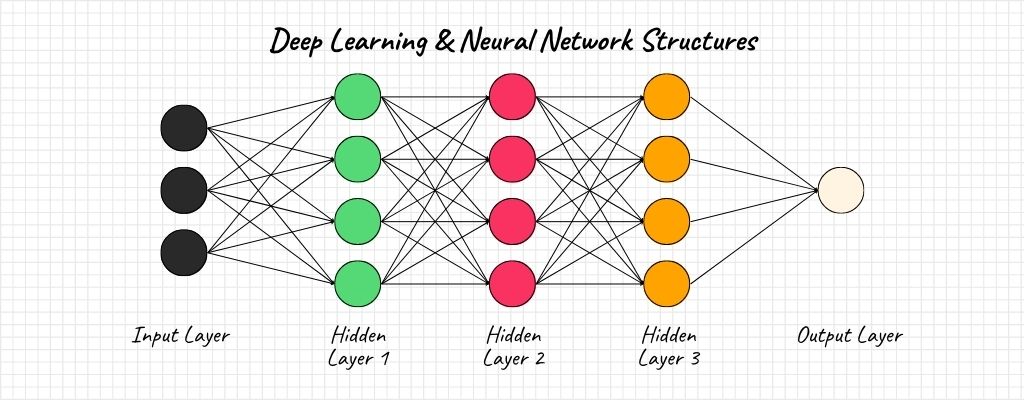
Measuring Similarity (e.g., Cosine Similarity)

Ever wondered how algorithms determine if two articles are similar or if a song sounds like another? It’s by measuring the ‘closeness’ of their vectors.

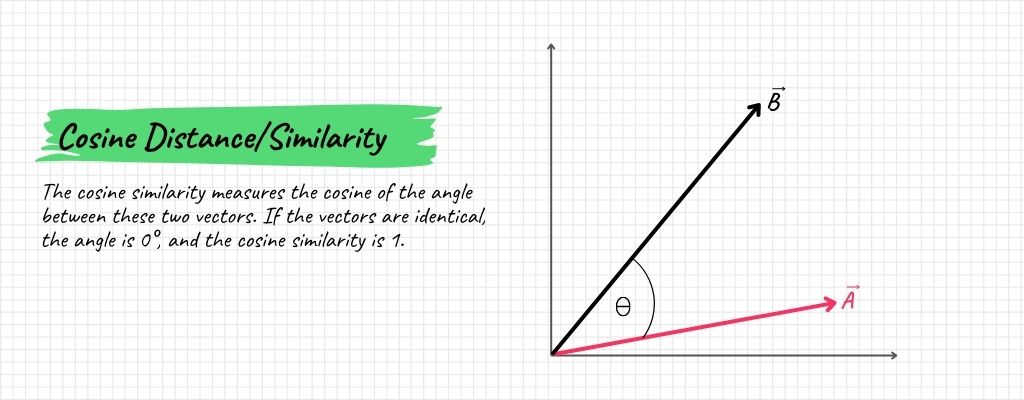
Cosine Similarity

One of my favorites! Imagine the vectors as arrows again. The cosine similarity measures the cosine of the angle between these two vectors. If the vectors are identical, the angle is 0°, and the cosine similarity is 1. If they’re utterly dissimilar, they’re orthogonal with an angle of 90°, and the cosine similarity is 0.

Mathematically, for two vectors \( \mathbf{A} \) and \( \mathbf{B} \):

\[ \text{Cosine Similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{||\mathbf{A}|| \times ||\mathbf{B}||} \]

Where \( \mathbf{A} \cdot \mathbf{B} \) is the dot product, and \( ||\mathbf{A}|| \) and \( ||\mathbf{B}|| \) are the magnitudes of the vectors.

By gauging such similarities, algorithms can cluster similar articles, recommend songs, and even match profiles on dating apps!

Importance of Studying Vector Spaces

As I ventured deeper into the realms of machine learning, one conviction solidified within me: that to truly grasp the elegance and prowess of machine learning algorithms, understanding vector spaces is paramount. It’s like understanding basic grammar rules before attempting to write an epic. 

Connection to Other Mathematical Concepts

Vector spaces serve as a bridge to many mathematical concepts, and my eureka moments often came when I uncovered these connections.

• Linear Algebra: Vector spaces are foundational to linear algebra. Concepts like linear independence, bases, and orthogonality are all interwoven with vector spaces. And trust me, linear algebra is the bread and butter of many machine learning algorithms!
• Calculus: When optimizing machine learning models, you’re often seeking minima or maxima – which takes you straight into the arms of differential calculus. Vectors and vector spaces make these concepts tangible.
• Probability and Statistics: Ever wondered how vectors come into play when gauging uncertainties? Concepts like multivariate distributions or covariance matrices thrive on vector spaces.

Building Strong Foundations

A well-built house requires a robust foundation, and the intricate world of machine learning is no different.

• Conceptual Clarity: Many get swayed by the allure of building fancy models but falter when they don’t deliver as expected. A deep understanding of vector spaces provides clarity, enabling you to troubleshoot and refine models effectively.
• Interdisciplinary Projects: Today, machine learning isn’t just the domain of computer scientists. Biologists, economists, sociologists – professionals from varied fields are leveraging it. Understanding vector spaces equips you to collaborate and contribute significantly to interdisciplinary projects.
• Future Learning: With a robust understanding of vector spaces, you’re well-poised to grasp more advanced concepts, be it quantum computing, advanced neural architectures, or the next big thing in machine learning.

In hindsight, my journey into machine learning would have been riddled with more challenges and ambiguities had I not invested time in understanding vector spaces. As you forge ahead, remember: every hour spent grasping these foundations will pay dividends in insights, breakthroughs, and genuine comprehension.

Real-world Examples of Vector Spaces

Theoretical concepts always seemed to settle in when complemented by real-world examples. There’s magic in seeing the theories take form and produce tangible results. In this section, let’s go on an explorative journey through some real-world applications to see vector spaces in action.

• Digital Marketing and SEO: Every digital marketer understands the importance of keywords, but few realize the role vector spaces play. Search engines often represent web pages and queries as vectors. By calculating the cosine similarity between a query vector and web page vectors, search engines rank pages in terms of relevance.
• Finance: When assessing the health and potential of stocks or assets, professionals often rely on historical data. By treating each stock’s historical performance as a vector, patterns emerge, helping in predicting future behaviors.
• Medicine: In gene expression studies, genes can be represented as vectors where each dimension corresponds to a particular experimental condition. Vector space techniques then allow researchers to find genes with similar or divergent behaviors.

Case Studies

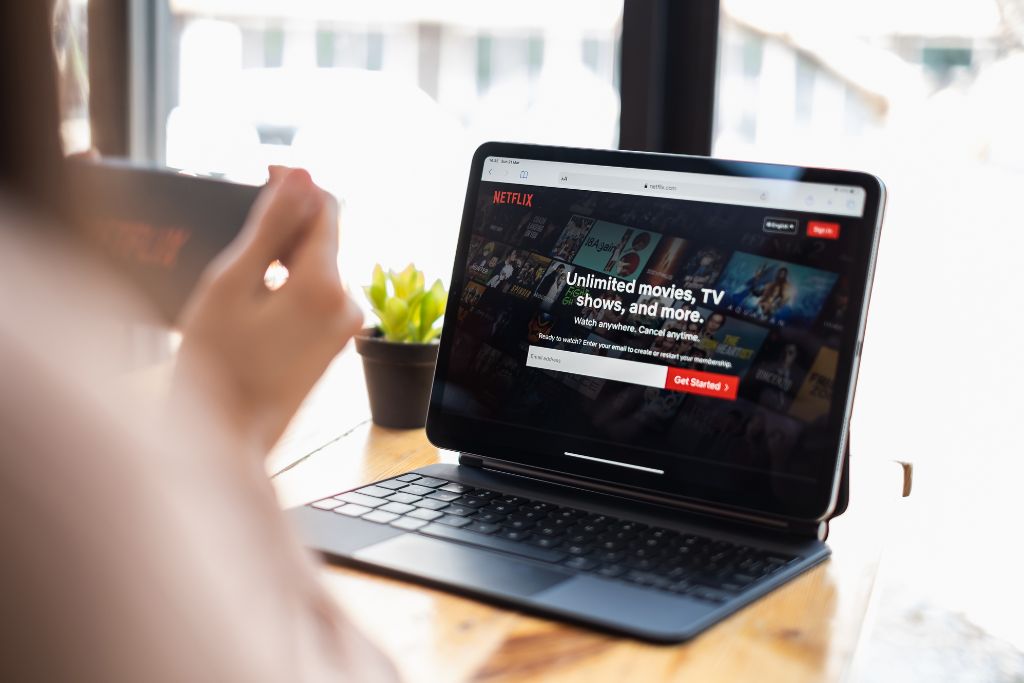
• Movie Recommendations – Netflix: Netflix’s recommendation system stands as a beacon of success. They represent each user and movie as vectors in a space. By measuring vector distances or similarities, they suggest movies that a user is likely to enjoy. The robustness of this system is so significant that Netflix once offered a million-dollar prize for anyone who could improve their recommendation algorithm by a mere 10%!
• E-Commerce – Amazon: Ever wondered how Amazon’s “Customers who bought this item also bought” works? It’s a dance of vectors again. Each product and user is a vector. By comparing user vectors to product vectors, Amazon finds products that align closely with a user’s purchasing habits.
• Music Streaming – Spotify: Spotify’s Discover Weekly, which provides song recommendations, utilizes vector representations of songs. By mapping songs in a vector space, it identifies and suggests tracks that are ‘near’ your musical taste.

Vector spaces, while mathematical and abstract, pulse at the heart of many modern technological marvels. Their applications span industries, breaking boundaries, and unveiling possibilities. 

As you proceed, let these case studies be a testament to the power and potential of vector spaces. Their magic lies in translating intricate real-world complexities into a language machines can understand and act upon. The wonders we witness today are just the tip of the iceberg; there’s so much more to explore and achieve.

Conclusion and Further Studies

Our journey through the landscape of vector spaces in machine learning has been extensive, enlightening, and I hope, invigorating. Before we wrap up, let’s take a moment to reflect on our path, while also casting an eye towards the horizon of deeper explorations. Here’s a recap of the key concepts in this article.

• Vector Representation: Whether it’s the words in a text, pixels of an image, or the melodies of a song, representing them as vectors equips machines to understand and manipulate them.
• Mathematical Foundations: Linear algebra, calculus, and probability intertwine seamlessly with vector spaces, rendering them pivotal to the entire scaffolding of machine learning.
• Applications: From the algorithms forming the bedrock of machine learning, like Linear Regression and Neural Networks, to advanced applications like recommendation systems, vector spaces play a starring role.
• Real-world Impacts: Through case studies, we observed how industries – from entertainment to finance – harness the power of vector spaces to drive innovation and deliver value.

The world of machine learning is vast and ever-evolving. The deeper you dive, the more wonders you uncover. Vector spaces, while foundational, are just a single piece of this intricate puzzle. With this knowledge under your belt, you’re better equipped to understand more complex topics and challenges in the field. Remember, every expert was once a beginner. Persistence, curiosity, and continuous learning are your best allies.

Our exploration of vector spaces, while comprehensive, is but an introduction to the vast world of machine learning. As you march ahead, treasure the insights you’ve gained, and let your insatiable curiosity be your guide. Here’s to many more eureka moments and the endless joy of learning!