In the world of machine learning, numbers take on more dimensions—literally. Meet vectors, the multi-dimensional arrows that point the way to complex computations, data representation, and algorithms. Vectors are not merely lists of numbers; they are mathematical entities with properties that make them indispensable in machine learning and linear algebra.
The objectives of this article are manifold. First, we aim to demystify what vectors are, both in mathematical terms and geometric interpretations. Then, we’ll delve into the key operations that involve vectors, such as arithmetic operations, dot products, and scalar multiplication. These operations aren’t just theoretical constructs; they form the building blocks of many machine learning algorithms.
So, whether you’re a student scratching your head about why your computer science curriculum includes linear algebra or a professional eager to delve into machine learning, this article is your starting point. Let’s embark on this mathematical journey that holds the keys to unlocking the intricate world of machine learning.

Section 1: Importance of Linear Algebra in Machine Learning
Linear algebra isn’t just a subject to be glossed over; it’s a foundational pillar in the world of machine learning. At first glance, the connection might not be apparent. Linear algebra, after all, is often associated with solving systems of linear equations, a topic seemingly far removed from building intelligent machines. However, it’s precisely this mathematical framework that powers the underlying algorithms, making machine learning possible, efficient, and scalable.
Relevance in Machine Learning Algorithms
Machine learning algorithms, in essence, are sets of rules or instructions that allow computers to learn from data. But how does this data get processed? Vectors and matrices—fundamental constructs in linear algebra—are the answer. They serve as compact data structures that can be manipulated easily. Operations like matrix multiplication or vector dot product are not merely academic exercises; they’re computational shortcuts that make large-scale data processing feasible.
For instance, consider support vector machines (SVM), an algorithm used in classification tasks. It utilizes hyperplanes to segregate different classes, and these hyperplanes are defined using vectors. In deep learning, backpropagation—a method for training neural networks—is fundamentally rooted in matrix operations. These concepts are just the tip of the iceberg.
Other Real-world Examples
Image Recognition
In image recognition tasks, an image is often represented as a multi-dimensional array (or tensor), where each element corresponds to a pixel’s color value. This tensor is, in reality, a higher-order generalization of vectors and matrices. When you apply convolutional neural networks (CNNs) for image recognition, numerous matrix multiplications and transformations occur behind the scenes.
Natural Language Processing (NLP)
When it comes to NLP, techniques like word embeddings convert words into vectors. The similarity between words or phrases can then be calculated using vector operations like cosine similarity. In advanced models like transformers, linear algebra plays an even more crucial role, facilitating operations at the heart of attention mechanisms.

Section 2: Defining a Vector
Vectors are often introduced as “arrows” or “directional quantities” that have both a magnitude and a direction. This definition provides an intuitive geometric understanding. However, vectors also have a more abstract mathematical definition that allows for more extensive applications in machine learning.
Mathematical Definition
Mathematically, a vector \( \vec{v} \) in a three-dimensional space can be represented as:
\[ \vec{v} = a\hat{i} + b\hat{j} + c\hat{k} \]
Here, \( a, b, \) and \( c \) are the components of the vector, and \( \hat{i}, \hat{j}, \) and \( \hat{k} \) are the unit vectors along the x, y, and z-axes, respectively. This equation gives us a tool for working with vectors algebraically, allowing for various operations and manipulations.
Geometric Interpretation
Geometrically, a vector is represented as an arrow with a certain length (magnitude) and direction. The tail of the arrow signifies the vector’s point of origin, while the head points towards its direction. The length of the arrow represents the vector’s magnitude.
Types of Vectors
Row Vectors and Column Vectors: These are vectors represented as single-row or single-column matrices. A row vector is typically written as \( [a, b, c] \), while a column vector is written as
\[ \begin{pmatrix}a \\b \\c\end{pmatrix}\]
Zero Vectors: A zero vector is a vector with all its components equal to zero. It is the additive identity in the vector space.
Unit Vectors: These are vectors with a magnitude of 1. The unit vectors \( \hat{i}, \hat{j}, \) and \( \hat{k} \) are fundamental examples.
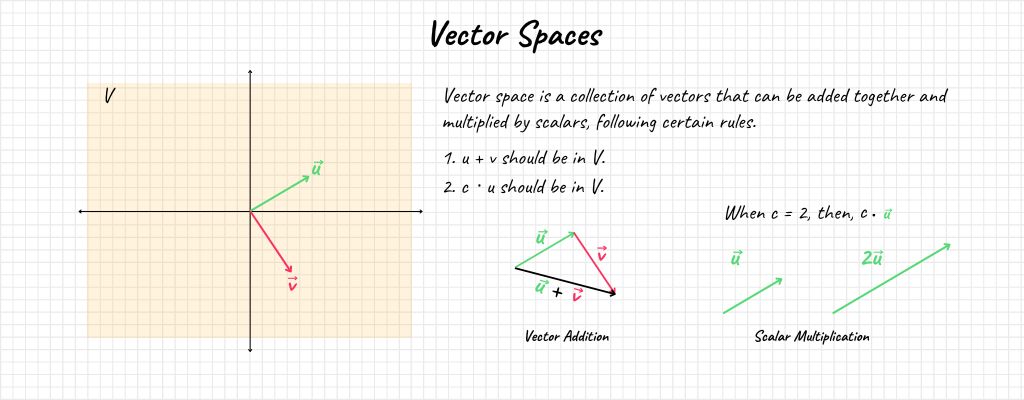
Vector Spaces
A vector space is a set of vectors that is closed under vector addition and scalar multiplication. This means that if \( \vec{a} \) and \( \vec{b} \) are vectors in a vector space, then \( \vec{a} + \vec{b} \) and \( c\vec{a} \) (where \( c \) is a scalar) must also belong to the same vector space.
Section 3: Vector Arithmetic Operations
The ability to manipulate vectors through arithmetic operations is a cornerstone of linear algebra and machine learning. While the operations may appear simple, their properties and applications in algorithms and data transformations are extensive.
Basic Operations
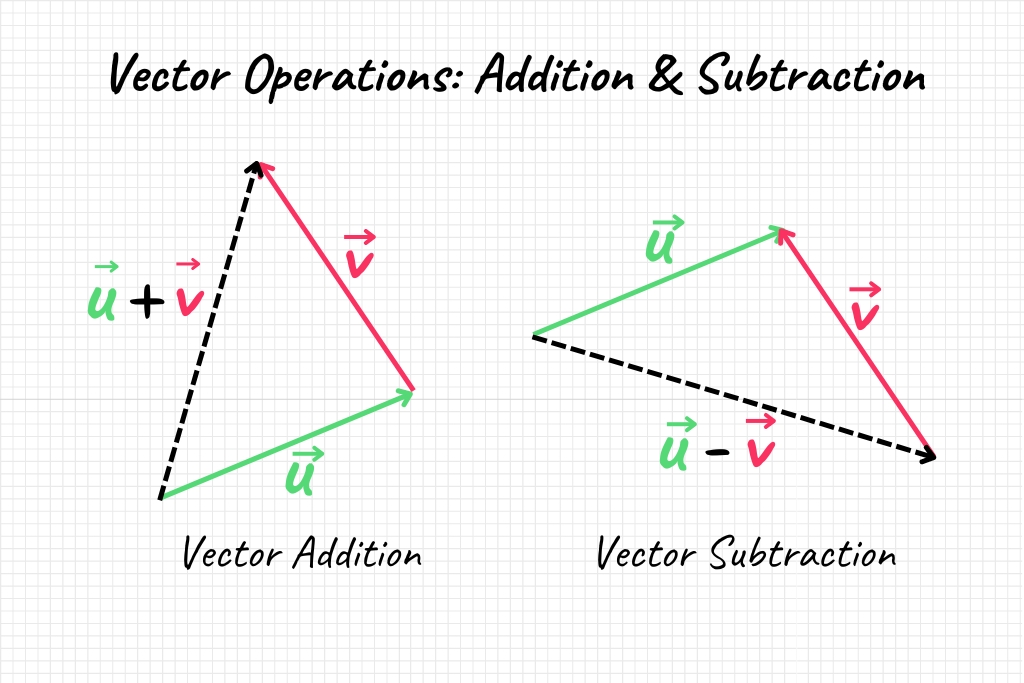
Vector Addition: The addition of two vectors \( \vec{a} \) and \( \vec{b} \) results in a new vector \( \vec{c} \).
\[ \vec{a} + \vec{b} = \vec{c} \]
In terms of components, if \( \vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k} \) and \( \vec{b} = b_1\hat{i} + b_2\hat{j} + b_3\hat{k} \), then,
\( \vec{c} = (a_1+b_1)\hat{i} + (a_2+b_2)\hat{j} + (a_3+b_3)\hat{k} \)
Vector Subtraction: The subtraction of \( \vec{b} \) from \( \vec{a} \) yields a new vector \( \vec{d} \).
\[ \vec{a} – \vec{b} = \vec{d} \]
Component-wise, \( \vec{d} = (a_1-b_1)\hat{i} + (a_2-b_2)\hat{j} + (a_3-b_3)\hat{k} \).
Properties of Vector Operations
Vector addition and subtraction are commutative and associative:
- Commutative: \( \vec{a} + \vec{b} = \vec{b} + \vec{a} \)
- Associative: \( (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \)
Examples and Use-cases in Machine Learning
- Data Transformation: Vector addition can be used in feature scaling and data normalization, essential steps in data preprocessing.
- Gradient Descent: Vector subtraction is crucial in algorithms like gradient descent, used for optimizing models and algorithms. The update rule involves subtracting a fraction of the gradient vector from the current point to find the minimum of a function.
- NLP and Word Embeddings: In Natural Language Processing, vector addition can be used to find word relationships. For example, the famous \( \text{“King”} – \text{“Man”} + \text{“Woman”} = \text{“Queen”} \) relationship is discovered through vector operations.
Section 4: Vector Dot Products
The dot product, sometimes called the scalar product, is a fundamental operation that takes two vectors and returns a single scalar. This operation is instrumental in various aspects of both mathematics and machine learning, from projecting vectors to computing similarity between entities.
The Concept of Dot Product
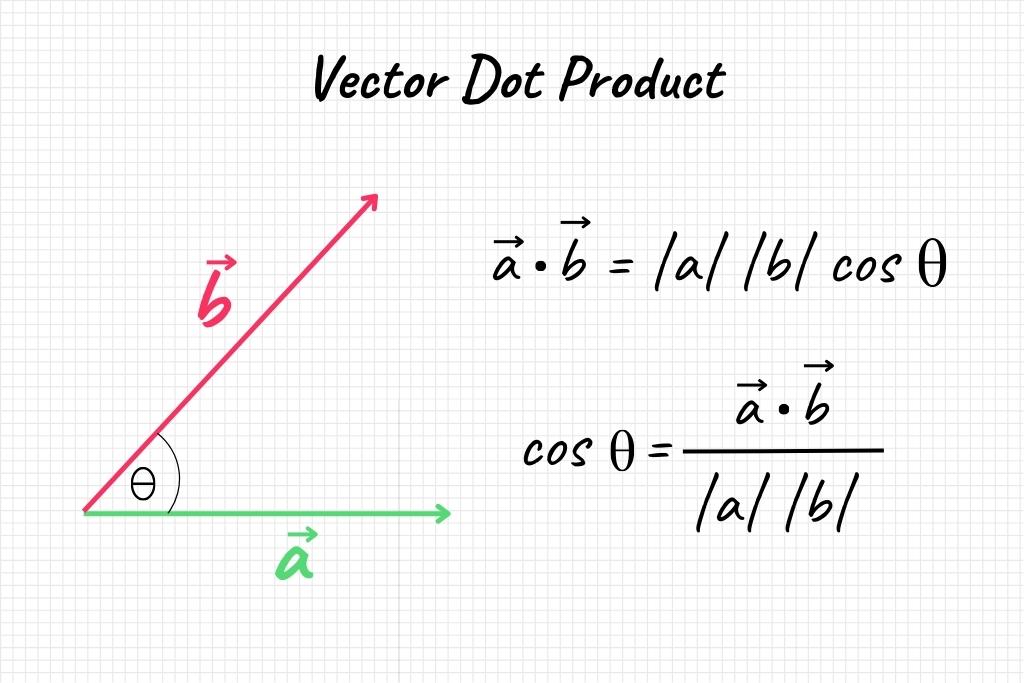
The dot product of two vectors \( \vec{a} \) and \( \vec{b} \) can be geometrically interpreted as the projection of one vector onto another. Algebraically, it’s a way to multiply vectors that result in a scalar.
\[\vec{a} \cdot \vec{b} = |\vec{a}| \times |\vec{b}| \times \cos(\theta)\]
Here, \( |\vec{a}| \) and \( |\vec{b}| \) are the magnitudes of vectors \( \vec{a} \) and \( \vec{b} \), respectively, and \( \theta \) is the angle between them.
The equation can also be represented in component form as:
\[\vec{a} \cdot \vec{b} = a_1 \times b_1 + a_2 \times b_2 + a_3 \times b_3\]
Applications of Vector Dot Products
- Cosine Similarity: In Natural Language Processing (NLP), the dot product is used to calculate cosine similarity, a measure of how similar two vectors (or documents) are.
- Image Recognition: In computer vision, dot products can be used in convolutional operations, essential for feature learning and image recognition.
- Dimensionality Reduction: Dot products are fundamental in techniques like Principal Component Analysis (PCA), used for reducing the dimensionality of data while preserving as much variability as possible.
Section 5: Vector-Scalar Multiplication
Vector-scalar multiplication is the operation of scaling a vector by a scalar quantity. It involves multiplying each component of the vector by a scalar to produce a new vector. This operation is invaluable for modifying the magnitude of vectors without altering their direction, making it critical for various data operations.
Conceptual Understanding
When we multiply a vector \( \vec{a} \) by a scalar \( c \), each component of \( \vec{a} \) is multiplied by \( c \), resulting in a new vector \( \vec{b} \).
\[c\vec{a} = \vec{b}\]
In component form, if \( \vec{a} = a_1\hat{i} + a_2\hat{j} + a_3\hat{k} \), then \( \vec{b} = c \times a_1\hat{i} + c \times a_2\hat{j} + c \times a_3\hat{k} \).
Applications of Vector-Scalar Multiplication
- Feature Scaling: In machine learning, particularly in algorithms that use distance measures like k-NN, vector-scalar multiplication is used to normalize or scale features so they all have the same influence on the model.
- Learning Rates: In optimization algorithms such as Gradient Descent, a learning rate (which is a scalar) multiplies the gradient vector to determine the next point in the search for a minimum or maximum. This process is crucial for algorithm convergence.
- Data Augmentation: Multiplying vectors by scalars can also be a simple method for data augmentation in fields like image recognition, essentially resizing images without changing their essential features.
- Regularization: Scalar multiplication is often used in regularization techniques to penalize large coefficients in a model, helping to prevent overfitting.
- Eigenvalue Problems: In Principal Component Analysis (PCA) and other dimensionality reduction techniques, scalar multiplication of eigenvectors by eigenvalues is a fundamental operation.
Section 6: Variations and Special Types of Vectors
Understanding the different kinds of specialized vectors and their properties is integral to mastering machine learning. These vectors have specific characteristics that make them useful in various algorithms and applications.
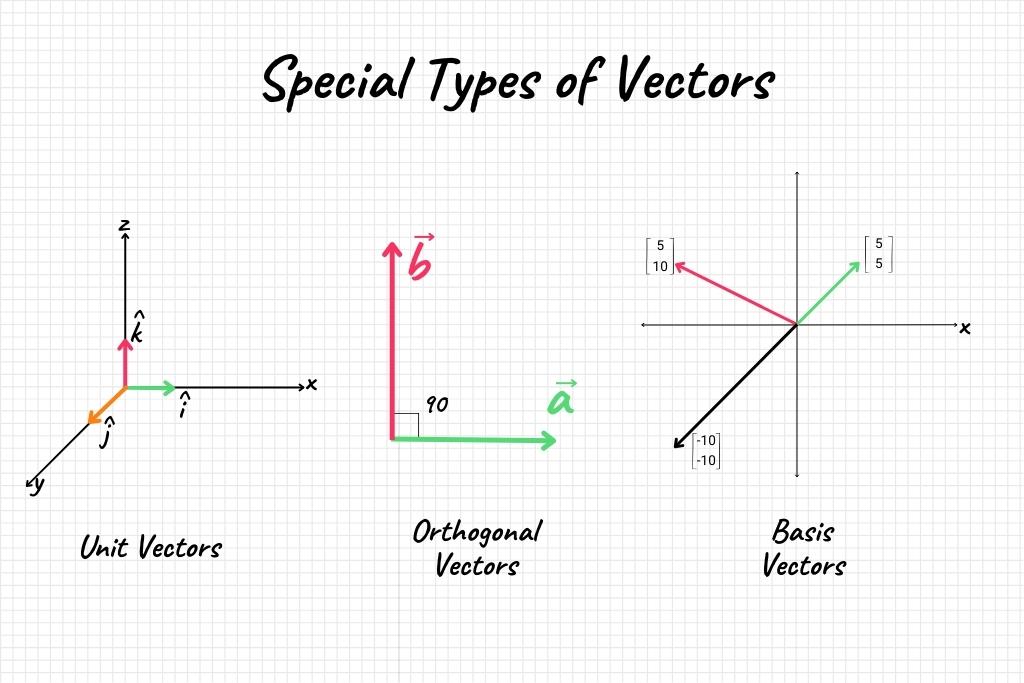
Unit Vectors
A unit vector is a vector with a magnitude of 1 and is usually denoted as \( \hat{u} \). It’s useful in maintaining direction without affecting magnitude.
\[\hat{u} = \frac{\vec{a}}{|\vec{a}|}\]
For example, in NLP tasks like text classification, converting word vectors to unit vectors can make it easier to compare the similarity between different documents.
Orthogonal Vectors
Orthogonal vectors are vectors that are perpendicular to each other, meaning their dot product is zero.
\[\vec{a} \cdot \vec{b} = 0\]
In machine learning, particularly in the context of PCA or Singular Value Decomposition (SVD), orthogonal vectors can serve as the basis of the transformed feature space. They are also used in algorithms like QR decomposition for solving linear equations.
Basis Vectors
Basis vectors are a set of vectors that can be linearly combined to create any vector in a particular space. In a 2D space, the standard basis vectors are \( \hat{i} \) and \( \hat{j} \).
In Support Vector Machines, finding the basis vectors—also known as support vectors—is crucial for defining the optimal hyperplane that separates different classes.
Applications of Special Types of Vectors
- Data Transformation: Unit vectors and basis vectors are often used in data transformation methods like PCA to reduce dimensionality or to convert data to a different basis.
- Clustering Algorithms: Orthogonal vectors can be useful in clustering algorithms like k-means to find orthogonal (and thus maximally distinct) cluster centroids.
- Text Similarity: Unit vectors are crucial in text similarity algorithms where you want to focus on the angle between vectors rather than their magnitudes.
Conclusion
Vectors and their operations form the backbone of machine learning. They act as the mathematical underpinning that makes complex algorithms not only feasible but also efficient and effective. Understanding vectors—from their basic definitions to arithmetic operations— enables you to grasp how machine learning algorithms manipulate data to produce meaningful results.
Key Takeaways
- Defining a Vector: A vector is a mathematical and geometric entity that has both magnitude and direction. The general equation for a vector is \( \vec{v} = a\hat{i} + b\hat{j} + c\hat{k} \).
- Vector Arithmetic Operations: Addition and subtraction of vectors are elementary yet crucial operations. The relevant equations are \( \vec{a} + \vec{b} = \vec{c} \) for addition and \( \vec{a} – \vec{b} = \vec{d} \) for subtraction.
- Dot Product: The dot product helps in measuring the angle between vectors and is particularly useful in similarity measures in machine learning. The governing equation is \( \vec{a} \cdot \vec{b} = |\vec{a}| \times |\vec{b}| \times \cos(\theta) \).
- Vector-Scalar Multiplication: Multiplying a vector by a scalar changes its magnitude but not its direction. It is frequently used for feature scaling and optimization in machine learning algorithms. The relevant equation is \( c\vec{a} = \vec{b} \).
- Special Types of Vectors: Unit vectors, orthogonal vectors, and basis vectors have unique properties and applications in machine learning, including data transformation and algorithm optimization.
By delving into each of these facets, you’ve equipped yourself with the foundational knowledge essential for progressing in machine learning. Whether you’re a student perplexed by the role of linear algebra in your curriculum or a professional making a career transition, understanding vectors is not just a theoretical requirement but a practical necessity.
Vectors are more than a mathematical concept; they’re a tool that unlocks the full potential of machine learning algorithms. From simple linear regression to complex neural networks, vectors make it all possible. As you continue your journey in machine learning, remember that a strong grasp of vectors and their operations will be one of your most valuable assets.

