In the world of data science and machine learning, mathematical concepts often serve as the bedrock on which algorithms and models are built. One such fundamental concept is that of vector norms, a measure that quantifies the “size” or “length” of vectors. Understanding vector norms is not merely an academic exercise; it’s crucial for various practical applications ranging from data preprocessing to optimization in machine learning algorithms.
In this article, you’ll have a thorough understanding of what vector norms are, including types like the L1, L2, and Vector Max Norms, and how to apply them in the context of data science and machine learning. Whether you’re a novice machine learning student or an expert in the field, this article will serve as your guide to the fundamentals.
In the sections that follow, we’ll delve into the mathematical intricacies of vector norms, offering definitions and formulae, as well as practical examples. We’ll explore the L1 Norm, which is widely used for sparsity in feature selection; the L2 Norm, commonly utilized in regularization to prevent overfitting; and the Vector Max Norm, which finds applications in various optimization problems. Finally, we’ll circle back to discuss the pervasive role of vector norms in the broader landscape of machine learning and data science.
So, let’s embark on this mathematical journey that promises to enhance your skills and deepen your understanding of machine learning algorithms.
What Are Vector Norms?
Vector norms are mathematical functions that measure the “magnitude” or “length” of a vector. In simpler terms, a vector norm quantifies how big a vector is. This is not to be confused with the dimensionality of a vector, which is the number of elements it contains. Rather, the norm captures the vector’s size in a way that can be considered as an extension of the idea of “distance” from the origin to the point represented by the vector in an n-dimensional space.
The Mathematical Representation of a Vector Norm
Mathematically, a vector norm is a function \( f: \mathbb{R}^n \rightarrow \mathbb{R} \) that maps a vector \( x \) with elements \( (x_1, x_2, …, x_n) \) to a real number, often denoted as \( \| x \| \). The function \( f \) satisfies the following properties:
- Non-negativity: \( \| x \| \geq 0 \) and \( \| x \| = 0 \) if and only if \( x = 0 \)
- Scalability: \( \| a \cdot x \| = |a| \cdot \| x \| \) for any scalar \( a \)
- Triangle Inequality: \( \| x + y \| \leq \| x \| + \| y \| \) for any vectors \( x \) and \( y \)
The general formula for a vector norm can be represented as:
\[ \| x \| = f(x_1, x_2, …, x_n) \]
Detailed Example: Euclidean Norm
To better understand vector norms, let’s take the example of the most commonly used norm, the Euclidean Norm (or L2 Norm). For a vector \( x = [x_1, x_2, …, x_n] \), the Euclidean Norm is calculated as:
\[\| x \|_2 = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}\]
Imagine you have a vector \( x = [3, 4] \) in a 2-dimensional space. Using the Euclidean Norm formula, the norm of \( x \) would be:
\[\| x \|_2 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]
The result \( \| x \|_2 = 5 \) gives us the length of the vector, essentially representing the distance from the origin (0,0) to the point (3,4) in 2D space.
Understanding vector norms is essential for a wide array of applications in data science and machine learning, including optimization techniques, regularization, and even in evaluating the performance of models.
Types of Vector Norms
Vector norms serve as the mathematical foundation for a variety of algorithms and techniques in machine learning and data science. Although they all share common properties, different types of vector norms are uniquely suited for distinct applications. Broadly, vector norms can be categorized into the following types:
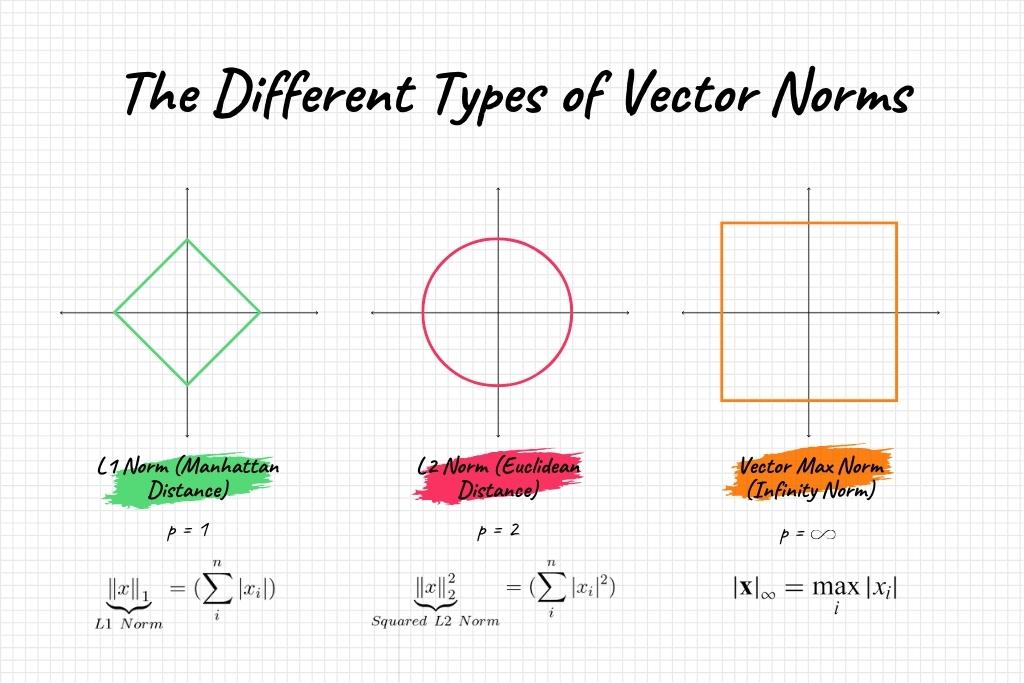
- L1 Norm (Manhattan or Taxicab Norm)
- L2 Norm (Euclidean Norm)
- Infinity Norm (Max Norm)
- p-Norms (Generalized Lp Norms)
L1 Norm (Manhattan or Taxicab Norm)
The L1 Norm is defined as the sum of the absolute values of the components of the vector.
\( \| x \|_1 = \sum_{i=1}^{n} |x_i| \)
L2 Norm (Euclidean Norm)
The L2 Norm is the square root of the sum of the squares of the components of the vector.
\( \| x \|_2 = \sqrt{\sum_{i=1}^{n} x_i^2} \)
Infinity Norm (Max Norm)
The Infinity Norm, also known as Max Norm, is simply the maximum absolute value among the elements of the vector.
\( \| x \|_\infty = \max(|x_1|, |x_2|, …, |x_n|) \)
p-Norms (Generalized Lp Norms)
These are a family of norms defined by a parameter \( p \) that generalizes the L1 and L2 norms.
\( \| x \|_p = \left( \sum_{i=1}^{n} |x_i|^p \right)^{1/p} \)
Understanding the types of vector norms and their specific uses allows you to better navigate the complex landscape of machine learning and data science algorithms. Whether you’re aiming to optimize a model’s performance or select the most relevant features in a high-dimensional dataset, vector norms offer invaluable mathematical tools to achieve these goals.
Vector L1 Norm
The Vector L1 Norm, also known as the Manhattan Norm or Taxicab Norm, measures the “distance” a vector covers when movements are restricted to a grid-based path, akin to moving along the streets of a city like Manhattan. In more formal terms, the L1 Norm is the sum of the absolute values of each component of the vector.
Mathematical Representation
Mathematically, the L1 Norm for a vector \( x = [x_1, x_2, …, x_n] \) is defined as follows:
\[L1 Norm = \| x \|_1 = \sum_{i=1}^{n} |x_i|\]
This representation is a realization of the function \( f(x_1, x_2, …, x_n) \) in the general vector norm formula \( \| x \| = f(x_1, x_2, …, x_n) \), specifically tailored for L1 Norm.
Practical Examples & Applications
Feature Selection: In high-dimensional datasets, feature selection is crucial. When used as a regularization term, the L1 Norm has the property of encouraging sparsity. For instance, in Lasso Regression (Least Absolute Shrinkage and Selection Operator), the L1 Norm is added as a penalty term to the loss function. This often results in some feature coefficients becoming zero, effectively eliminating them from the model.
\[Loss Function = \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 + \lambda \sum_{i=1}^{p} |w_i|\]
Here \( \lambda \) is the regularization parameter, \( w_i \) are the feature weights, \( y_i \) are the actual values, and \( \hat{y}_i \) are the predicted values.
Sparsity in Neural Networks: L1 Norm is sometimes used in the hidden layers of neural networks to induce sparsity. Here, sparsity means that a lot of neurons will output zero, making the network simpler and easier to interpret.
Anomaly Detection: In algorithms like the one-class SVM, the L1 Norm can be used to measure how far a new data point is from the center of the existing data points. If the L1 Norm exceeds a certain threshold, the data point is considered an anomaly.
Optimization: Some linear programming problems use the L1 Norm as an objective to be minimized, especially when we are interested in minimizing the sum of absolute errors.
By understanding the L1 Norm’s mathematical underpinnings and its applications, you’re equipped to make informed decisions in feature selection, model regularization, and even anomaly detection. Its utility in creating sparse models makes it particularly useful in situations where computational efficiency and model interpretability are of paramount importance.

Vector L2 Norm
The Vector L2 Norm, commonly referred to as the Euclidean Norm, is perhaps the most intuitive way to measure the “length” of a vector, extending the Pythagorean theorem to multi-dimensional spaces. It computes the straight-line distance from the origin to the point identified by the vector in the vector space.
Mathematical Representation
For a given vector \( x = [x_1, x_2, …, x_n] \), the L2 Norm is mathematically defined as:
\[L2 Norm = \| x \|_2 = \sqrt{\sum_{i=1}^{n} x_i^2}\]
Here, each component of the vector \( x \) is squared, summed together, and then square-rooted. This mathematical formalization gives us the Euclidean distance of the vector from the origin.
Practical Examples and Applications
Distance Metrics: The L2 Norm serves as the mathematical basis for the Euclidean distance, commonly employed in clustering algorithms like k-means and in classification algorithms like k-nearest neighbors (K-NN). The Euclidean Distance formula between two points \( A \) and \( B \) is expressed as:
\[d(A, B) = \sqrt{\sum_{i=1}^{n} (A_i – B_i)^2}\]
Regularization: In Ridge Regression, the square of the L2 Norm of the coefficients is used as a penalty term. This constrains the size of the coefficients and thus prevents overfitting.
\[Loss Function = \sum_{i=1}^{n} (y_i – \hat{y}_i)^2 + \lambda \sum_{i=1}^{p} w_i^2\]
Here, \( \lambda \) is the regularization parameter and \( w_i \) are the feature weights.
Optimization Algorithms: Gradient descent techniques often use the L2 Norm to measure the size of the gradient. If the L2 Norm of the gradient is very small, it can indicate that the algorithm has reached a minimum.
Natural Language Processing (NLP): In document classification or sentiment analysis tasks, the L2 Norm can be used to normalize text vectors, ensuring that all documents are represented fairly, irrespective of their length.
Image Recognition: In convolutional neural networks (CNNs), the L2 Norm can be used to penalize the activation functions, encouraging them to map the input image into a space that is easier for the network to interpret.
By delving into the L2 Norm, its mathematical formulation, and its versatile applications, you gain another crucial tool in your machine learning arsenal. This norm is particularly useful when you need a straightforward measure of distance or magnitude, or when you are looking to apply regularization techniques to mitigate the risks of overfitting.

Vector Max Norm
The Vector Max Norm, also known simply as the Infinity Norm (\( \infty \)-norm), measures the “size” of a vector by taking the maximum absolute value among its components. Unlike the L1 and L2 Norms, which consider every element of the vector in their calculations, the Max Norm focuses solely on the element with the greatest magnitude.
Mathematical Representation
For a vector \( x = [x_1, x_2, …, x_n] \), the Max Norm is mathematically expressed as:
\[Max Norm = \| x \|_\infty = \max(|x_1|, |x_2|, …, |x_n|)\]
Here, the \( \max \) function selects the largest absolute value among all the components \( |x_1|, |x_2|, …, |x_n| \) of the vector.
Practical Examples and Applications
Weight Regularization: The Max Norm is commonly used as a constraint on the weights in neural networks. By constraining the maximum value that any weight can take, one can prevent “exploding gradients,” a problem wherein the gradients become too large for the model to converge during training.
\[w_{new} = \min\left(1, \frac{\| w \|_\infty}{r}\right) w\]
Here, \( \| w \|_\infty \) is the Max Norm of the weight vector \( w \), and \( r \) is the maximum allowed value for \( \| w \|_\infty \).
Optimization: In some optimization problems, especially those involving resource allocation, the objective function might involve maximizing or minimizing the maximum amount of a resource used. Here, the Max Norm can be applied as the objective function.
Matrix Norms: When extending norms to matrices, the Max Norm can also be useful. In this setting, it helps to analyze the impact of an operator on a vector space.
Chebyshev Distance: In clustering or classification tasks, the Max Norm can be used to compute the Chebyshev distance between points, which may be appropriate for certain types of data structures, such as chess boards. The Chebyshev Distance between two points \( A \) and \( B \) is expressed as:
\[d(A, B) = \max(|A_1 – B_1|, |A_2 – B_2|, …, |A_n – B_n|)\]
By understanding the Max Norm, you add another layer to your comprehension of how to measure vectors and apply these measures in machine learning tasks. Whether you’re concerned with weight regularization, optimization, or specialized distance metrics, the Max Norm offers a focused, highly specific tool for your needs.

Finding Vector Norms in Python
Python is a go-to language for machine learning and data science, thanks in part to libraries like NumPy that make it easier to work with mathematical operations. In this section, we’ll explore how to compute the L1, L2, and Max Norms of vectors using Python.
Finding the Vector L1 Norm
The L1 Norm of a vector can be found using NumPy’s `numpy.linalg.norm()` function with the argument `ord=1`.
import numpy as np
# Create a vector
vector = np.array([1, 2, 3])
# Compute the L1 Norm
l1_norm = np.linalg.norm(vector, ord=1)
print("L1 Norm of the vector:", l1_norm)Upon execution, this will output an L1 norm of 6.0. Here, \( L1 Norm = |1| + |2| + |3| = 6.0 \).
Finding the Vector L2 Norm
For the L2 Norm, you’d use the same function but set `ord=2`.
# Compute the L2 Norm
l2_norm = np.linalg.norm(vector, ord=2)
print("L2 Norm of the vector:", l2_norm)This will yield a norm of approximately 3.74. Mathematically, \( L2 Norm = \sqrt{1^2 + 2^2 + 3^2} \approx 3.74 \).
Finding the Vector Max Norm
For the Max Norm, the `ord` parameter should be set to `np.inf`.
# Compute the Max Norm
max_norm = np.linalg.norm(vector, ord=np.inf)
print("Max Norm of the vector:", max_norm)Executing this code snippet will give you a max norm of 3.0. This aligns with \( Max Norm = \max(|1|, |2|, |3|) = 3 \).
In summary, Python—especially with the help of the NumPy library—provides a straightforward and efficient way to compute various vector norms. These are essential tools in the toolkit of anyone working in data science and machine learning.
Key Takeaways
- Understanding Vector Norms: The article delved into the concept of vector norms, which are a measure of the “length” or “magnitude” of vectors. We discussed the mathematical representation of vector norms, generally given by \( \| x \| = f(x_1, x_2, …, x_n) \).
- Types of Vector Norms: We explored the L1, L2, and Max Norms, each with its unique properties and mathematical representations.
- L1 Norm: \( \sum_{i=1}^{n} |x_i| \)
- L2 Norm: \( \sqrt{\sum_{i=1}^{n} x_i^2} \)
- Max Norm: \( \max(|x_1|, |x_2|, …, |x_n|) \)
- Applications in Data Science & Machine Learning: Vector norms are crucial in data preprocessing, machine learning algorithms, and regularization techniques. They’re used in normalization, k-NN, SVM, neural networks, and methods like L1 and L2 regularization.
- Python Implementations: We also learned how to find these norms using Python’s NumPy library, a practical skill that you can apply immediately in your data science projects.
After reading this article, you should not only have a theoretical understanding of vector norms but also know how to apply them practically in data science and machine learning tasks.
Conclusion
The understanding of vector norms is indispensable for anyone venturing into the realm of data science and machine learning. These mathematical tools serve as the backbone for various algorithms, influencing everything from data preprocessing to model performance. Furthermore, mastering vector norms paves the way for a more in-depth grasp of other advanced topics, making you better equipped to tackle complex problems in the field.
While this article provides a comprehensive overview, the subject of vector norms is vast and ever-evolving. Therefore, I encourage you to delve deeper into the topic and its nuanced applications. Whether you are a novice enthusiast or a seasoned professional, an intimate understanding of vector norms will undeniably enrich your skill set.
Feel free to explore more, implement these concepts in your projects, and continue on your path to becoming an expert in data science and machine learning.