Linear Independence of Vectors

In the vast landscape of mathematics and computing, vectors stand as fundamental building blocks that permeate a variety of disciplines. From physics and engineering to data science and machine learning, the versatile nature of vectors makes them indispensable. But vectors don’t operate in isolation. Their interactions often give rise to complex mathematical spaces and structures. One of the most crucial properties that govern these interactions is what mathematicians call “linear independence.” 

Understanding linear independence isn’t merely an academic exercise; it holds practical significance, especially in fields like data science and machine learning. Grasping this concept equips you with the foundational knowledge to deal with a multitude of challenges. For instance, when you’re selecting features for a machine learning model, identifying linearly independent variables can mean the difference between a model that accurately predicts outcomes and one that’s saddled with redundancies.

In this article, we’ll embark on a comprehensive exploration of linear independence. You’ll learn its formal definition, methods to determine it, and most importantly, its applications in the thriving fields of data science and machine learning. Whether you’re a novice machine learning enthusiast or a professional looking to refresh your understanding of this pivotal concept, this article aims to serve as a robust reference point.

Section 1: What is Linear Independence?

In the realm of linear algebra, the concept of linear independence serves as a cornerstone for understanding vector spaces, matrices, and much more. But what does it mean for a set of vectors to be linearly independent? Let’s delve into its definition, mathematical formulation, and the conditions that must be met for vectors to be deemed linearly independent.

Definition of Linear Independence

Linear independence is a property of a set of vectors whereby no vector in the set can be expressed as a linear combination of the other vectors. In simpler terms, each vector in the set contributes something unique to the overall structure of the vector space. They are like pillars holding up a structure; remove one, and the structure loses an element of its integrity.

Mathematical Formulation

The mathematical criterion for a set of vectors \( \vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n \) to be linearly independent is expressed as follows:

\[c_1\vec{v}_1 + c_2\vec{v}_2 + \ldots + c_n\vec{v}_n = \vec{0}\]

In this equation, \( c_1, c_2, \ldots, c_n \) are scalars. For the vectors to be linearly independent, the only solution to this equation must be:

\[c_1 = c_2 = \ldots = c_n = 0\]

If any other combination of \( c_1, c_2, \ldots, c_n \) can satisfy the equation, then the vectors are not linearly independent; they are linearly dependent.

Conditions for Vectors to be Linearly Independent

To check whether a set of vectors is linearly independent, you can employ a few different methods. Here are some key conditions that must be met:

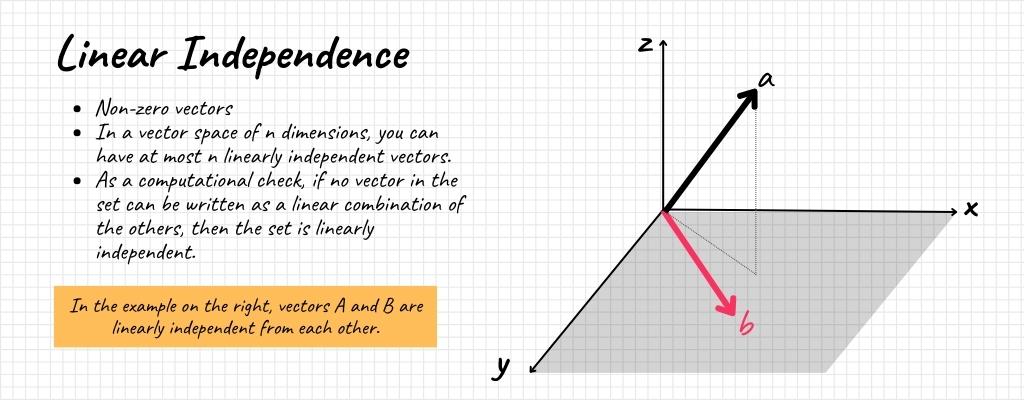
• Non-zero Vectors: A set containing the zero vector can never be linearly independent because the zero vector can always be represented as a linear combination of other vectors with zero as the scalar.
• Number of Vectors vs. Dimensions: In a vector space of \( n \) dimensions, you can have at most \( n \) linearly independent vectors. 
• Determinant of the Matrix: If the vectors are represented as columns in a square matrix, that matrix is invertible (i.e., its determinant is not zero) if and only if the columns are linearly independent.
• Row Reduced Echelon Form: When you transform the matrix representing the vectors into row-reduced echelon form, you should not get a row of zeros for the set to be linearly independent.
• Linear Combination: As a computational check, if no vector in the set can be written as a linear combination of the others, then the set is linearly independent.

Understanding the intricacies of linear independence is paramount for navigating complex problems in data science and machine learning. The conditions outlined above serve as mathematical safeguards to ensure the robustness of various computational procedures.

Section 2: How to Determine Linear Independence

Determining linear independence is more than just an academic exercise; it’s a practical skill that has real-world applications, especially in the realm of data science and machine learning. Various methods can be employed to ascertain whether a set of vectors is linearly independent. In this section, we’ll focus on two predominant techniques—row reduction to echelon form and using the determinant of a matrix—supplemented with examples that offer step-by-step walkthroughs.

Row Reduction and Echelon Form

Row reduction is a powerful tool for investigating the linear independence of vectors. By transforming a given set of vectors into row-echelon form or reduced row-echelon form, we can ascertain whether the vectors are linearly independent.

Here’s a basic outline of the procedure:

• Create the Matrix: Assemble the vectors as columns in a matrix \( A \).
• Row Reduce: Use elementary row operations to row-reduce \( A \) to its row-echelon or reduced row-echelon form.
• Examine the Rows/Columns: If there’s a “leading 1” for each column, the columns of the original matrix are linearly independent. On the other hand, if any columns of the row echelon form did not contain a leading 1, then the original column vectors would then be linear dependent.

For instance, consider the vectors \( \vec{v}_1 = [1, 2, 3] \) and \( \vec{v}_2 = [4, 5, 6] \). The matrix formed by these vectors is:

\[A = \begin{pmatrix}1 & 4 \\2 & 5 \\3 & 6\end{pmatrix}\]

Upon row reduction, we get:

\[A = \begin{pmatrix}1 & 4 \\0 & 1 \\0 & 0\end{pmatrix}\]

Since each column has a leading 1 coefficient, \( \vec{v}_1 \) and \( \vec{v}_2 \) are linearly independent.

Using the Determinant of a Matrix

Another method to determine linear independence is through the determinant of a matrix. This approach is specifically useful when dealing with square matrices.

• Square Matrix: Form a square matrix \( A \) by making the vectors its columns.
• Calculate Determinant: Compute the determinant \( \text{Det}(A) \).
• Examine Determinant: If \( \text{Det}(A) \neq 0 \), then the vectors are linearly independent.

Let’s assume we have vectors \( \vec{v}_1 = [1, 0] \) and \( \vec{v}_2 = [0, 1] \). The square matrix \( A \) becomes:

\[A = \begin{pmatrix}1 & 0 \\0 & 1\end{pmatrix}\]

The determinant \( \text{Det}(A) = 1 \), which is not zero. Thus, \( \vec{v}_1 \) and \( \vec{v}_2 \) are linearly independent.

The above methods and examples provide a robust framework for identifying linear independence in sets of vectors, a critical skill when you’re dealing with feature selection, algorithm optimization, and data representation in machine learning.

Section 3: Linear Independence vs. Linear Dependence

Both linear independence and linear dependence are fundamental concepts in linear algebra that describe the relationships among vectors within a set. Understanding the nuances between these two terms is crucial, especially when you’re handling large datasets or designing machine learning algorithms. In this section, we will define linear dependence, provide its mathematical formulation, and contrast it with linear independence to create a comprehensive understanding of these core concepts.

Definitions and Mathematical Formulations for Linear Dependence

Linear dependence, in contrast to linear independence, is the property where at least one vector in a set can be expressed as a linear combination of the other vectors. Simply put, if you have a set of vectors and one of them doesn’t provide any new ‘direction’ or ‘information’ not already present in the other vectors, that set is linearly dependent.

The mathematical formulation for linear dependence is similar to that of linear independence:

\[c_1\vec{v}_1 + c_2\vec{v}_2 + \ldots + c_n\vec{v}_n = \vec{0}\]

In this equation, if you can find any set of scalars \( c_1, c_2, \ldots, c_n \) not all equal to zero that satisfies the equation, then the vectors are linearly dependent. In other words, for a set to be linearly dependent, the equation should have a non-trivial solution where at least one \( c_i \neq 0 \).

Image

Comparing and Contrasting the Two

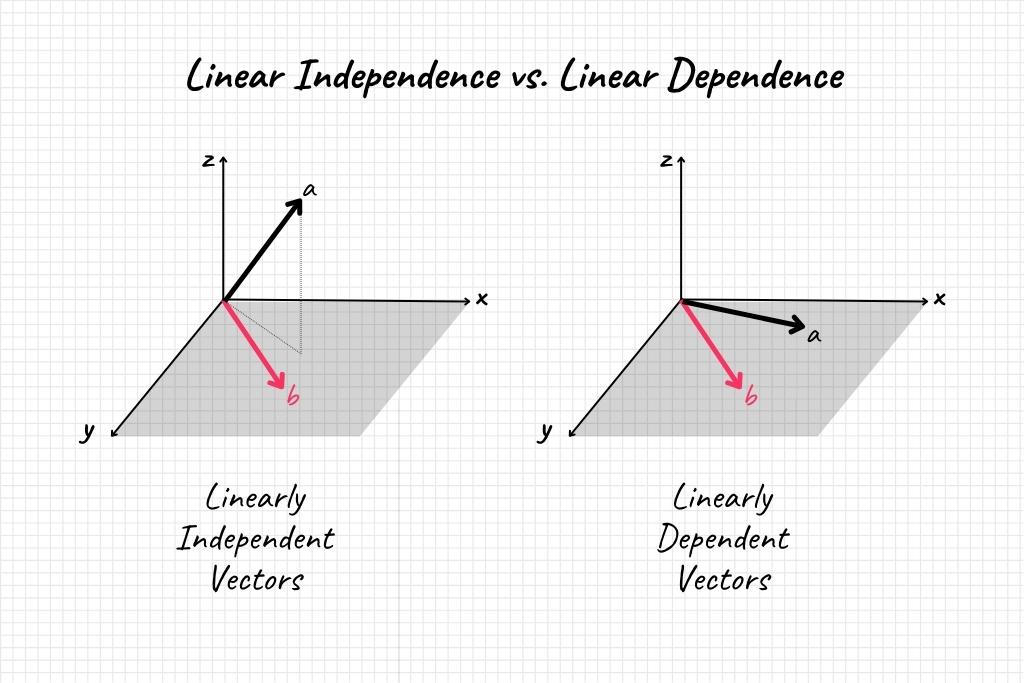
1. Uniqueness of Representation: In a linearly independent set, each vector offers unique information, making it impossible to express any one vector as a linear combination of the others. In contrast, a linearly dependent set contains at least one vector that can be described as such a combination.
2. Mathematical Solution: For linear independence, the only solution to \( c_1\vec{v}_1 + c_2\vec{v}_2 + \ldots + c_n\vec{v}_n = \vec{0} \) is the trivial one where all \( c_i = 0 \). For linear dependence, a non-trivial solution exists.
3. Determinant of the Matrix: If the determinant of the matrix formed by the vectors as columns is zero, the vectors are linearly dependent. If the determinant is non-zero, they are independent.
4. Redundancy: Linear dependence implies redundancy in data, which is often undesirable in machine learning models, as it can lead to overfitting. Linear independence, on the other hand, suggests that each vector (or feature in a machine learning context) contributes something unique, which is generally more desirable.
5. Dimensionality: In a vector space of dimension \( n \), you can have at most \( n \) linearly independent vectors, but you can have more than \( n \) linearly dependent vectors.
6. Row Reduction: Both linear independence and linear dependence can be verified using row reduction techniques, but the criteria for each are different, as outlined in previous sections.

Understanding the distinction between these two concepts is crucial in fields like data science and machine learning, where the interplay of features, dimensions, and data can dramatically impact the performance of models and algorithms.

By grasping the differences between linear independence and linear dependence, you not only deepen your understanding of linear algebra but also gain critical insights into how this knowledge is applicable in real-world problems, particularly in data science and machine learning.

Section 4: Practical Applications of Linear Independence

Understanding the properties of vectors and their linear independence or dependence has significant implications in the field of data science, especially in optimizing machine learning models and handling large datasets.

Feature Selection in Machine Learning Models

When we talk about feature selection, we’re essentially discussing the elimination of redundant or irrelevant variables from the dataset. Linear independence is a valuable criterion here. If features are linearly dependent, removing some of them may lead to a simpler, yet equally predictive, model. Simplifying models not only improves computation time but can also mitigate the risk of overfitting.

Dimensionality Reduction Techniques like PCA

Principal Component Analysis (PCA) is a statistical method used to reduce the dimensionality of data. One of its primary aims is to find a set of new uncorrelated variables (Principal Components) that are linear combinations of the original variables. These Principal Components essentially form a set of linearly independent vectors that capture the most significant patterns in the data.

Representing Data in a Reduced Feature Space

In line with PCA and feature selection, the ultimate goal is to represent data in a reduced feature space without losing critical information. Through methods like PCA, or even simpler techniques like matrix factorization, one can transform the original set of possibly dependent vectors into a new set of linearly independent vectors that capture the essence of the data.

Basis of Vector Spaces in Natural Language Processing

In Natural Language Processing (NLP), vector spaces are used to represent text data. Understanding the basis and dimension of these spaces is crucial, and the concept of linear independence is fundamental to forming a basis.

Orthogonalization Processes in Algorithms

Algorithms like the Gram-Schmidt process utilize orthogonalization to convert a set of linearly independent vectors into orthogonal or orthonormal vectors. This is particularly useful in optimization algorithms and even in machine learning algorithms like QR decomposition.

Section 5: FAQs

Section 6: Key Takeaways

The concept of linear independence serves as a foundational pillar in linear algebra, extending its implications into various scientific and technological disciplines. For anyone looking to specialize in data science or machine learning, mastering this concept is non-negotiable. Its core principles are instrumental in performing feature selection, dimensionality reduction, and even in the basic formulation of several machine learning algorithms. 

Understanding linear independence isn’t merely an academic exercise; it’s a prerequisite for anyone seriously considering a career or specialization in data science and machine learning. This article has provided an in-depth exploration of the topic, highlighting its mathematical underpinnings and drawing connections to practical applications. Through examples and analyses, it’s evident that whether you’re looking to optimize feature selection in data models or understand the structural nuances in machine learning algorithms, linear independence serves as a critical component. Thus, mastering this concept can significantly elevate your analytical capabilities, setting you on the path to becoming an expert in your field.